Puntos Extras... Nuevo Algoritmo Cuantico

Pues navegando por internet llege a dar con una noticia interesante, en el cual han creado, Un algoritmo cuántico que permitiría resolver sistemas de ecuaciones lineales muy rápidamente.

Aram W. Harrow de University of Bristol y Avinatan Hassidim y Seth Lloyd del MIT proponen un algoritmo cuántico para resolver este tipo de problemas(sistemas de ecuaciones lineales).

El algoritmo se basa en la ventaja que los qubits tienen frente a los bits, pues pueden estar en una superposición de estados y ser “0″ y “1″ a la vez. El algoritmo codifica en una superposición todas las posibles soluciones del sistema, englobando todos los posibles valores de las constantes que están al lado derecho del sistema de ecuaciones (la b de antes). A partir de esta solución universal se puede extraer la solución particular que se busca sin necesidad de calcularla.

La ganancia de tiempo sería enorme. Si con un ordenador convencional tratamos de resolver un sistema de N ecuaciones tardaremos como mínimo 1000 veces más si N es 1000 veces más grande. Pero con el nuevo algoritmo se haría mucho más rápido, aunque N sea muy grande, pues la dificultad del problema no crecería en este caso con N.
Aunque todavía no hay ordenadores cuánticos, Lloyd especula con la posibilidad de aplicar pronto este método de manera indirectamente en Astronomía para obtener imágenes libres de defectos al aprovecharse de la naturaleza cuántica de los fotones.

No deja de ser curioso que desde hace tiempo se viene intentando crear sin éxito algoritmos cuánticos que resuelvan problemas de tipo NP rápidamente (que crecen no polinómicamente según aumenta el tamaño del problema) y que, sin embargo, ahora se proponga uno para un problema mucho más sencillo, pero quizás más práctico.

Puntos Extras... Algoritmo Euclidiano

<>

Definicion:

Pues principalmente el algoritmo de Euclides es un método simple y eficaz para encontrar el máximo común divisor entre dos números enteros diferentes de cero. Este algoritmo no requiere factorización.

El MCD de dos números enteros es el mayor entero que divide a ambos, mientras que el resto, el algoritmo de Euclides se basa en el principio de que el MDC no cambia si el menor número se resta de la más grande.

Ejemplo Paso a Paso:

Encontrar el MCD de 252 y 105:

OBTENEMOS COMO RESULTADO 21.

Animacion del algoritmo:

Otro ejemplo para que quede mucho mejor explicado:

Calcularemos el MCD de 348 y 156:

348	156
-312 36 ≠ 0	2

¿De qué otra no es cero, reemplazamos el dividendo y el divisor:

156	36
-144 12 ≠ 0	4

¿De qué otra no es cero, reemplazamos el dividendo y el divisor:

36	12
-36 0	3

Así que el máximo común divisor de los 348 enteros y 156 es 12.

cociente	2	4	3
348	156	36	12
resto	36	12	0

TEOREMA DEL ALGORITMO:

Bibliografia:

http://es.wikipedia.org/wiki/M%C3%A1ximo_com%C3%BAn_divisor

http://www.unalmed.edu.co/~earamosn/cursos/matematicas_discretas_09II/plan/notas-AlgNum.pdf

http://pt.wikipedia.org/wiki/Algoritmo_de_Euclides

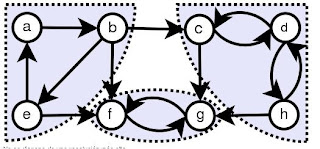
Puntos Extras...Algoritmo "Componente Conexo DFS"

Componente Conexo: Utilizando DFS

Definicion:

Pues principalmente se dice que un grafo dirigido es llamado fuertemente conexo.

si para cada par de vértices u y v existe un camino de u hacia v y un camino de v hacia u. Los componentes fuertemente conexos (CFC) de un grafo dirigido son sus subgrafos máximos fuertemente conexos. Estos subgrafos forman una partición del grafo.

Un subgrafo fuertemente conexo es máximo si contiene todos los vértices del grafo o si al agregarle un vértice cualquiera deja de ser fuertemente conexo.

Algoritmo:

Sea un grafo dirigido:

1. Aplicar búsqueda en profundidad sobre G
2. Calcular el grafo traspuesto.
3. Aplicar busqueda en profundidad sobre G^t (el grafo traspuesto) iniciando la búsqueda en los nodos de mayor a menor tiempo de finalización obtenidos en la primera ejecución de busqueda en profundidad (paso 1)
4. El resultado será un bosque de árboles. Cada árbol es una componente fuertemente conexa.

Para poder tener un mejor entendimiento del mismo pondre algunas definiciones:

Busqueda en Profundidad: es un algoritmo que permite recorrer todos los nodos de un grafo o arbol de manera ordenada, pero no uniforme. Su funcionamiento consiste en ir expandiendo todos y cada uno de los nodos que va localizando, de forma recurrente, en un camino concreto. Cuando ya no quedan más nodos que visitar en dicho camino, regresa, de modo que repite el mismo proceso con cada uno de los hermanos del nodo ya procesado.

Grafo traspuesto (GT) se define como:
GT = . Es interesante observar que G y GT tienen los mismos CFC. El algoritmo para CFC hace dos recorridos: uno del grafo G y otro del grafo GT en el segundo recorrido, los nodos se consideran en orden decreciente de f[]

Pseudocodigo DFS:

  DFS(grafo G)
   PARA CADA vertice u ∈ V[G] HACER
           estado[u] ← NO_VISITADO
           padre[u] ← NULO
   tiempo ← 0
   PARA CADA vertice u ∈ V[G] HACER
           SI estado[u] = NO_VISITADO ENTONCES
                   DFS_Visitar(u)

Complejidad:

La complejidad de este algoritmo es O(V+E). Ya que depende de la cantidad de aristas y de vertices que tenga dicho grafo.

Bibliografia:

-http://es.wikipedia.org/wiki/Algoritmo_de_c%C3%A1lculo_de_los_componentes_fuertemente_conexos_de_un_grafo

-http://docencia.udea.edu.co/regionalizacion/teoriaderedes/profundidad.html

-http://es.wikipedia.org/wiki/Teor%C3%ADa_de_grafos

Puntos Extras...Respuestas Modelo-3

<<Puntos Extras>>

Maquina Turing(Examen de Medio Curso)

Principalmente tendremos que convertir el 37 en número binario.

37 / 2 = 18 ----1

18/ 2= 9---------0

9/ 2= 4-----------1

4/ 2= 2-----------0

2/2= 1------------0

1/2=0-------------1

Obtenemos el número binario siguiente: 1OO1O1

Después lo situamos en la cinta de la maquina turing:

Se queda en estado “s” coloca un 0 y mueve a la derecha

Se queda en estado “s” valor 1 y avanza hacia la derecha

Se queda en estado “s” valor 0 y avanza hacia la derecha, hasta que encuentra una posición vacía en la cinta.

Se convierte en estado “t” se coloca un 0 y avanza hacia la izquierda

Se queda en estado “t” se valor 1 y avanza hacia la izquierda

Se cambia a “si” se convierte a 1 y ahí se detiene.

¿Qué es la salida de la maquina turing (decimal)?

-Al último tenemos como resultado en la cinta el siguiente número binario: 01001110

-Después la conversión de 01001110 es: 2⁶+2³+2²+2¹=78

¿Qué hace la maquina turing?

-Lo que hace la maquina turing es que, multiplica el numero por 2 (porque agrega un 0 en la ultima posición) y le suma, en este caso 4 ya que depende de la posición en el que se encuentra el primer 0 de izquierda a derecha.

¿Qué complejidad tiene?

-Su complejidad es de 0(n), ya que depende de la cantidad de pasos a realizar(n num).