Puntos Extras...Respuestas Modelo-2

<<Puntos Extras>>

Analisis Asintotico(Examen de Medio Curso)

Principalmente queremos obtener una cota superior asintótica ( O(f(n)) ) de la función g(n).

Para poder tener una idea de como debe quedar la cota, demostrare la grafica con la funcion g(n)

Tomaremos los primeros 4 valores de f(n) y g(n) para poder tener una base de funciones.

n ——–g(n)
3—–15
12—–170
30—–600
57—–1500

Para poder tener una cota superior podremos comprobar las siguientes funciones:

- F(x)= e^x

f(3)= e^3=20.08

f(12)= e^12=162,754.791

f(30)=e^30=1.013 x 10 ^13( un numero demasiado alto)

f(57)=e^57= ( un numero demasiado alto)

Descartaremos esta función ya que el número se eleva demasiado después del “3”.

- F(x)= 2^x

f(3)= 2^3=8

f(12)= 2^12=4096

f(30)=2^30= ( un numero demasiado alto)

f(57)=2^57= ( un numero demasiado alto)

Descartaremos esta función ya que el número se eleva demasiado después del “12”.

- F(x)= x^3

f(3)= 3^3=27

f(12)= 12^3=1728

f(30)=30^3= 27000

f(57)=57^3= 185193( un numero demasiado alto)

Descartaremos esta función ya que el número se eleva demasiado después del “30”.

- F(x)= x^2

f(3)= 3^2=9

f(12)= 12^2=144

f(30)=30^2=900

f(57)=57^2=3249

Descartaremos esta función ya que el número se eleva demasiado después del “57”.

- F(x)= n log (n)

f(3)= 3 log3=1.43

f(12)= 12 log12=12.95

f(30)=30 log 30=44.31

f(57)=57 log 57=100.08

Tendríamos que usar esta función ya que que no sobrepasa por mucho la función g(n) y tampoco no baja

demasiado como una función f(x)=x, asi que tomaremos esta función.

Calcularemos los demás valores, tomare los últimos tres para que haya un mejor balance.

- F(x)= n log (n)

f(5002)= 100000 log5002=369914.36

f(10393)= 200000 log10393=803,328.18

f(40039)=600000 log 40039=2,761489

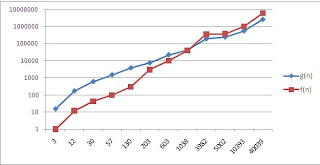
Asi queda la grafica con su correspondientes funciones f(g) y g(n):