Puntos Extras...Algoritmo "Componente Conexo DFS"

Componente Conexo: Utilizando DFS

Definicion:

Pues principalmente se dice que un grafo dirigido es llamado fuertemente conexo.

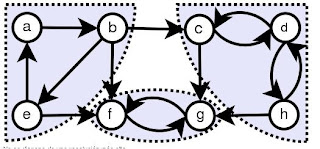
si para cada par de vértices u y v existe un camino de u hacia v y un camino de v hacia u. Los componentes fuertemente conexos (CFC) de un grafo dirigido son sus subgrafos máximos fuertemente conexos. Estos subgrafos forman una partición del grafo.

Un subgrafo fuertemente conexo es máximo si contiene todos los vértices del grafo o si al agregarle un vértice cualquiera deja de ser fuertemente conexo.

Algoritmo:

Sea un grafo dirigido:

1. Aplicar búsqueda en profundidad sobre G
2. Calcular el grafo traspuesto.
3. Aplicar busqueda en profundidad sobre G^t (el grafo traspuesto) iniciando la búsqueda en los nodos de mayor a menor tiempo de finalización obtenidos en la primera ejecución de busqueda en profundidad (paso 1)
4. El resultado será un bosque de árboles. Cada árbol es una componente fuertemente conexa.

Para poder tener un mejor entendimiento del mismo pondre algunas definiciones:

Busqueda en Profundidad: es un algoritmo que permite recorrer todos los nodos de un grafo o arbol de manera ordenada, pero no uniforme. Su funcionamiento consiste en ir expandiendo todos y cada uno de los nodos que va localizando, de forma recurrente, en un camino concreto. Cuando ya no quedan más nodos que visitar en dicho camino, regresa, de modo que repite el mismo proceso con cada uno de los hermanos del nodo ya procesado.

Grafo traspuesto (GT) se define como:
GT = . Es interesante observar que G y GT tienen los mismos CFC. El algoritmo para CFC hace dos recorridos: uno del grafo G y otro del grafo GT en el segundo recorrido, los nodos se consideran en orden decreciente de f[]

Pseudocodigo DFS:

  DFS(grafo G)
   PARA CADA vertice u ∈ V[G] HACER
           estado[u] ← NO_VISITADO
           padre[u] ← NULO
   tiempo ← 0
   PARA CADA vertice u ∈ V[G] HACER
           SI estado[u] = NO_VISITADO ENTONCES
                   DFS_Visitar(u)

Complejidad:

La complejidad de este algoritmo es O(V+E). Ya que depende de la cantidad de aristas y de vertices que tenga dicho grafo.

Bibliografia:

-http://es.wikipedia.org/wiki/Algoritmo_de_c%C3%A1lculo_de_los_componentes_fuertemente_conexos_de_un_grafo

-http://docencia.udea.edu.co/regionalizacion/teoriaderedes/profundidad.html

-http://es.wikipedia.org/wiki/Teor%C3%ADa_de_grafos